| جواهر ستار التعليمية |
| أهلا وسهلا بك زائرنا الكريم ، في منتديات جواهر ستار التعليميه المرجو منك أن تقوم بتسجـيل الدخول لتقوم بالمشاركة معنا. إن لم يكن لـديك حساب بعـد ، نتشرف بدعوتك لإنشائه بالتسجيل لديـنا . سنكون سعـداء جدا بانضمامك الي اسرة المنتدى مع تحيات الإدارة |
| جواهر ستار التعليمية |
| أهلا وسهلا بك زائرنا الكريم ، في منتديات جواهر ستار التعليميه المرجو منك أن تقوم بتسجـيل الدخول لتقوم بالمشاركة معنا. إن لم يكن لـديك حساب بعـد ، نتشرف بدعوتك لإنشائه بالتسجيل لديـنا . سنكون سعـداء جدا بانضمامك الي اسرة المنتدى مع تحيات الإدارة |
 |
|  |
أهلا وسهلا بك ضيفنا الكريم، إذا كانت هذه زيارتك الأولى للمنتدى، فيرجى التكرم بزيارة صفحة التعليمــات، بالضغط هنا كما يشرفنا أن تقوم بالتسجيل بالضغط هنا إذا رغبت بالمشاركة في المنتدى، أما إذا رغبت بقراءة المواضيع والإطلاع فتفضل بزيارة القسم الذي ترغب أدناه.
 الخميس 9 أكتوبر - 9:53:23 الخميس 9 أكتوبر - 9:53:23 | المشاركة رقم: | |||||||
Admin 
|  موضوع: المستوى : ثانية ثانوي السنة الدراسية : 2008 الشعبة :علوم تجريبية + رياضيات موضوع: المستوى : ثانية ثانوي السنة الدراسية : 2008 الشعبة :علوم تجريبية + رياضيات المستوى : ثانية ثانوي السنة الدراسية : 2008 الشعبة :علوم تجريبية + رياضيات 2009/ المستوى : ثانية ثانوي السنة الدراسية : 2008 الشعبة :علوم تجريبية + رياضيات و تقني رياضي حليلاتعمار { المحور: الاشتقاقية وتطبيقاتالاشتقاقية } أثبت باستعمال التعريف أن : (I (0 ( ) (1 0 lim2 3 3 h h ® ( 2 ) (2 ، + = 0 lim 2 1 1 h h h ® ( ) (3 ، + + = 1 lim2 3 5 x x ® + = ثم اكتب f ¢(a ) وعين العدد المشتق a ادرس قابلية اشتقاق الدوال التالية عند القيمة (02 و (T ) ثم ارسم المماس a ذات الفاصلة A عند النقطة (Cf ) للمنحني (T ) معادلة المماس (O;i , j ) في معلم متعامد ومتجانس (Cf ) المنحني urur (1 (2 ، a = -1 ، f (x ) = x 2 +1 f (x ) 1 x a =1 ، = (4 ، a = 4 ، f (x ) =1+ x (3 ( ) 3 1 1 f x x = + + a = 2 ، f (x )=x 2 - 2x + ب : 1 ¡ دالة معرفة على f (03 (O;i , j ) ينسب المستوي لمعلم متعامد ومتجانس urur f المنحني الممثل للدالة (Cf ) وليكن f ¢( واستنتج ( 2 x0 = قابلة للاشتقاق عند العدد 2 f 1) أثبت أن الدالة التي فاصلتها 2 A عند النقطة (Cf ) مماس المنحني (T ) 2) عين معادلة ل ثم أنجز جدول تغيرات [ ; 1 + ¥[ و ]-¥ 1; ] على المجالين f 3) ادرس اتجاه تغير الدالة f الدالة (Cf ) محور تناظر للمنحني x = 4) أثبت أن المستقيم الذي معادلته 1 (Cf ) ثم المنحني (T ) 5) ارسم المماس في كل حالة f للدالة f ¢(a ) استعمل التعريف لحساب العدد المشتق ( ( من الحالات المقترحة التالية : 1 ( ) 3 1 1 f x x = + + a = 0 ، a = 2 ، f (x ) = x 2 + x -1 (3 ، a = 4 ، f (x ) = x - 3 (2 10/ الصفحة 1 العددالمشتق –معادلةالمماس–التقريبالتآلفي Company Confidential حليلاتعمار ثم استنتج العدد h بدلالة العدد الحقيقي f (a + h) في كل حالة من الحالات التالية ، احسب (II .a من أجل f المشتق للدالة (1 a =1 ، a = 0 ، f (x ) = x 3 + 2x - 5 (2 ، a = 2 ، f (x ) = x 2 + x -1 (O;i , j ) 05 ) ينسب المستوي لمعلم متعامد ومتجانس urur المنحني الممثل للدالة (Cf ) وليكن المعرفة بالعبارة : f f (x ) 1 x = عند (Cf ) للمنحني (T1 ) عند القيمة 1 ثم اوجد معادلة المماس f 1) ادرس قابلية اشتقاق الدالة . النقطة ذات الفاصلة 1 عند (Cf ) للمنحني (T2 ) ثم اوجد معادلة المماس - عند القيمة 1 f 2) ادرس قابلية اشتقاق الدالة .- النقطة ذات الفاصلة 1 . (Cf ) ثم (T2 ) و (T1 ) 4) ارسم . (T2 ) يوازي (T1 ) 3) بين أن f (x )= 1+ x : دالة معرفة بالعبارة f (06 . عند 0 f 1) ادرس قابلية اشتقاق الدالة قريب من الصفر h 1 من اجل + h 2) استنتج احسن تقريب تآلفي للعبارة 3) عين قيمة مقربة للعدد 1.00024 1/ب رر التقريب التآلفي المحلي عند 0 في كل حالة من الحالات التالية : (07 ( ) أ ) 31. ب) 1 1 + x » 1+ 3x 2 + x » + x . ج) 1 1 1 x x » - . + 1 عين أحسن تقريب تآلفي للعدد 1(08 3 + h إلى الصفر h عندما يؤول 2/ باستعمال هذا التقريب جد قيمة تقريبية لكل من الأعداد : 1 3.02 ، 1 2.99 ، 1 3.1 (O;i , j ) ينسب المستوي لمعلم متعامد ومتجانس urur منحنيان معادلتيهما (D ) و (C ) . y = -4x - و 4 y = x على الترتيب : 2 عند نقطة يطلب تعيين إحداثياتها (C ) هو المماس ل (D ) 1) بين أن (C ) ثم (D ) 2) ارسم f (x )=6x 2 + 3x - دالة معرفة بالعبارة : 5 ¡ الكيفية من x عند القيمة 0 f 1) ادرس قابلية اشتقاق الدالة f ¢(x ) 2) استنتج f ( 3) استعمل التقريب التآلفي المماسي عند 1 لحساب قيمة مقربة للعدد ( 1.001 10/ الصفحة 2
| |||||||
 |
 السبت 21 مارس - 13:31:43 السبت 21 مارس - 13:31:43 | المشاركة رقم: | |||||||
عضو نشيط 
|  موضوع: رد: المستوى : ثانية ثانوي السنة الدراسية : 2008 الشعبة :علوم تجريبية + رياضيات موضوع: رد: المستوى : ثانية ثانوي السنة الدراسية : 2008 الشعبة :علوم تجريبية + رياضيات المستوى : ثانية ثانوي السنة الدراسية : 2008 الشعبة :علوم تجريبية + رياضيات شطراااااااااااااااااااااااااا
| |||||||
 |
| الإشارات المرجعية |
| الذين يشاهدون محتوى الموضوع الآن : 20 ( الأعضاء 3 والزوار 17) | |
|
| |
مواقع صديقة
| أعلانات نصية | |
| قوانين المنتدى | |
| إعــــــــــلان | إعــــــــــلان | إعــــــــــلان | إعــــــــــلان |

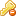 فقدت كلمة المرور؟
فقدت كلمة المرور؟ فقدت إسم العضوية؟
فقدت إسم العضوية؟










